Parameters Section
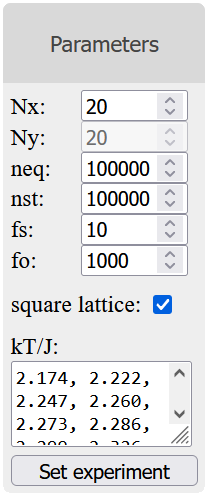
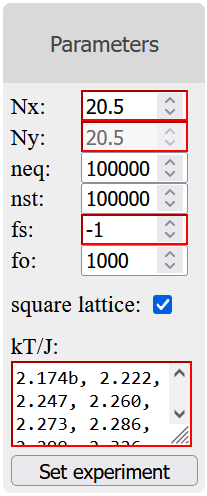
The parameters section, as shown in figures 3 and 4, allows the user to set up experiments.
Any invalid parameters that have been entered will be highlighted in red. A new experiment cannot be set up until these fields have been corrected.
| Param. |
Type |
Description |
| Nx |
Int (+) |
# lattice sites in x |
| Ny |
Int (+) |
# lattice sites in y |
| neq |
Int (+) |
# equilibration steps |
| nst |
Int (+) |
# statistics steps |
| fs |
Int (+) |
sample frequency |
| fo |
Int (+) |
output frequency |
| KT/J |
Float |
temperatures |
Table 1 - Input parameters.
Table 1 briefly describes the input parameters.
Quantities: \( n_{eq} \), \( n_{st} \), \( f_{s} \) and \( f_{o} \) are measured in units of "Monte Carlo steps per lattice site".
I.e., setting \( n_{eq} = m \) results in \( m \times N_{x} \times N_{y} \) total Monte Carlo steps.
This ensures that on average, each spin gets flipped the same number of times regardless of lattice size.
The simulations start by performing an equilibration period of length \( n_{eq} \).
This gives the systems time to reach thermal equilibrium and no statistics are collected during this period.
A statistics period of length \( n_{st} \) follows the equilibration period, during which samples of the systems' thermodynamic variables are taken every \( f_{s} \) steps.
Setting \( f_{s} \) too low causes subsequent samples to be highly correlated, which is detrimental to the averages.
Setting it too high makes the averages take a long time to converge and appear noisy.
The output frequency, \( f_{o} \), sets how often the results are sent to the screen from the various simulations.
Setting this number too low can make the chart animations appear jerky and, in the extreme, cause the configuration animations to start buffering .
Once valid parameters have been entered, clicking the "Set experiment" button will place a new experiment in the experiments section.
Multiple experiments can be set up at the same time, as shown in figures 5 and 6.
At this point, no simulations are running, they are simply in a state where they are waiting to be run.
Figure 3 - Input parameter fields.
Figure 4 - Invalid parameters.
Experiments Section
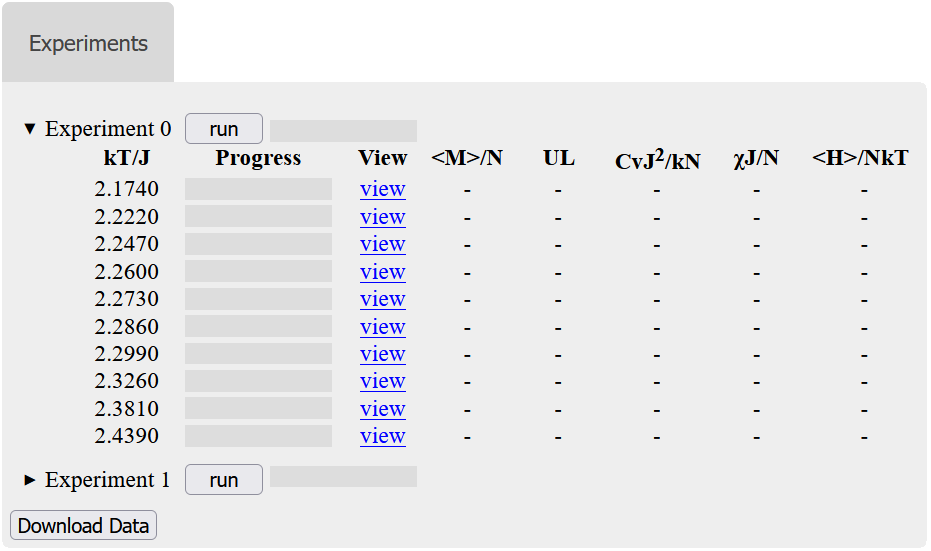
An experiment can be expanded by cliking on it to reveal a data grid, which is initially empty as in figure 5.
Each row in the data frame corresponds to an Ising model simulation, but note that the view links will not work until the experiment is running.
Figure 5 - The experiments section displaying two experiments that are waiting to be run. Experiment 0 has its data grid expanded.
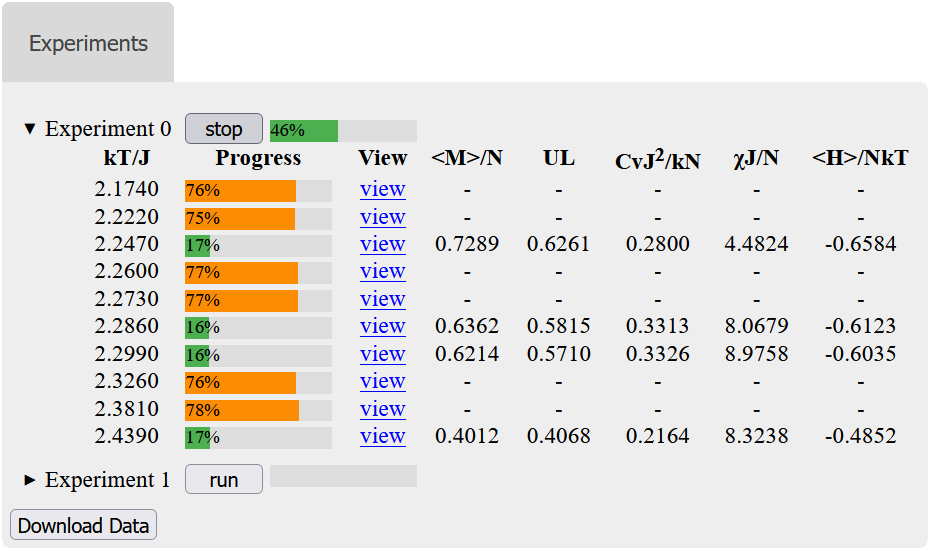
Figure 6 - The experiments section showing experiment 0 running with its data grid expanded. Experiment 1 is still waiting to be run.
Clicking on an experiment's 'run' button will start each of its consituent simulations.
Figure 6 shows a running experiment where some experiments are in the equilibration phase (orange progress bar) and some have entered the statistics phase (green progress bar).
The progress bar next to the 'run' button gives the total progress of the experiment as a whole.
Simulations that are in the statistics phase have their row of the data grid updated every \( f_{o} \) steps.
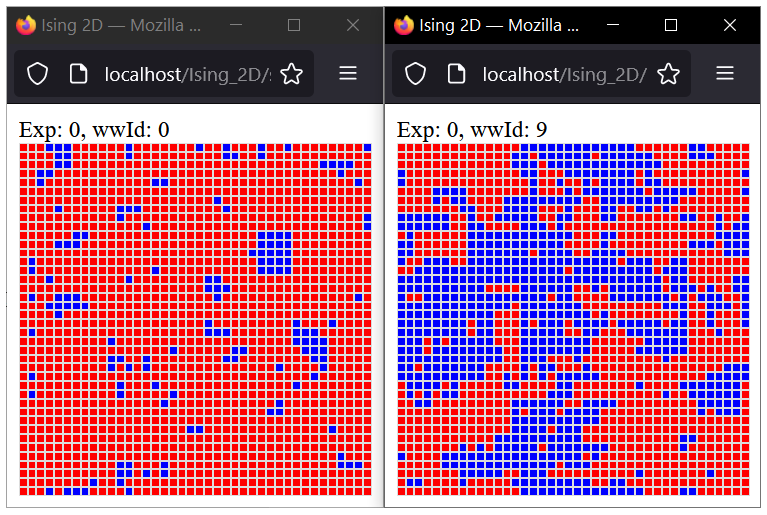
Once the experiment has started, clicking on one of the 'view' links will open a new window showing the current state of the configuration, as shown in figure 7.
If the experiment is running, the configuration animation will be updated every \( f_{o} \) steps.
Clicking the 'Download Data' button allows the user to download all simulation data up to that point as a tab-delimited text file.
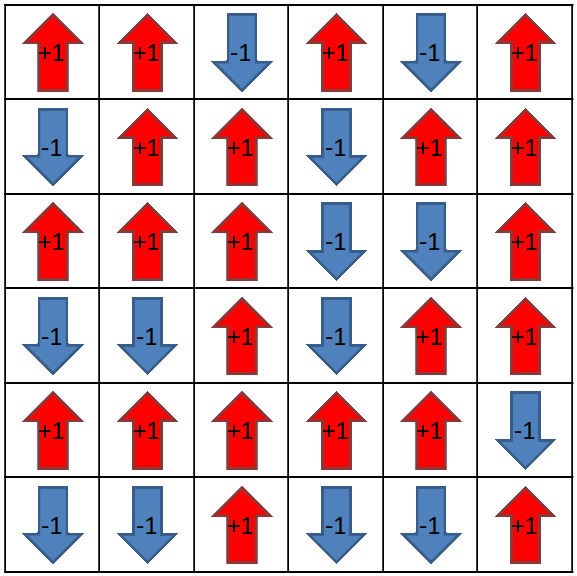
Figure 7 - Two (40x40) Ising model configurations at different temperatures, generated by clicking the 'view' links seen in figures 5 and 6.
Charts Section
Clicking the checkboxes in the 'charts' section shows/hides plots related to the various quantities detailed in table 2.
| Chart |
Description |
| \( \langle M \rangle / N \) |
Magnetisation (scaled) |
| \( U_{L} \) |
4th-order cumulant |
| \( C_{v}/(k_{B}N) \) |
Heat capacity (scaled) |
| \( \chi J / N \) |
Susceptibility (scaled) |
| \( \langle H \rangle / (Nk_{B}T) \) |
Energy (scaled) |
Table 2 - Quantities plotted on charts.
The charts display the results from the experiments that the user has started.
Each of the multiple data-series corresponds to a different experiment, which are updated every \(f_{o}\) steps throughout the simulation until it ends.
By displaying the results from experiments run at different lattice sizes, \( L=(N_{x}, N_{y}) \), on a single chart, the user is able to see both the quantity's temperature dependence and the effect of the finite-lattice size on the results.
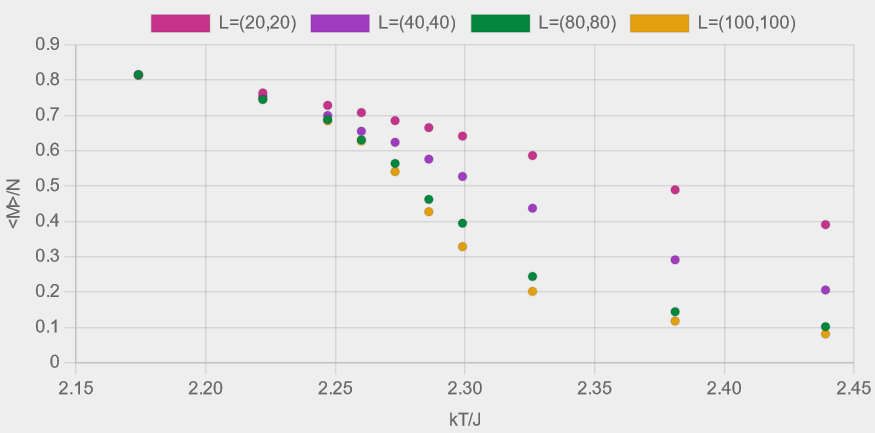
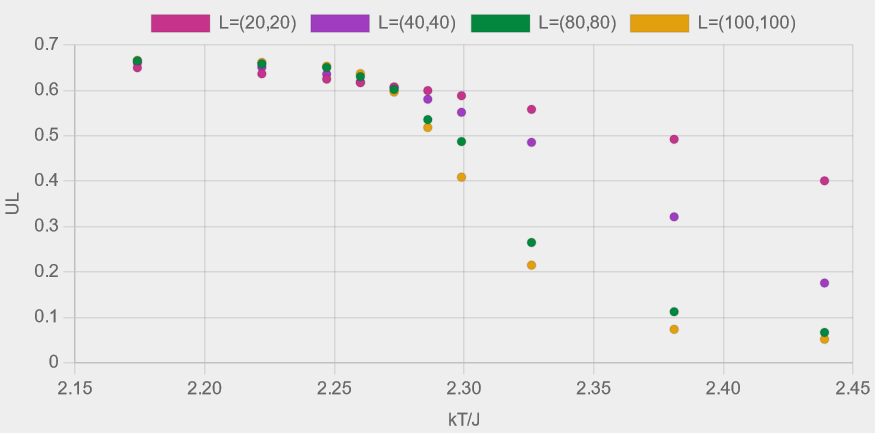
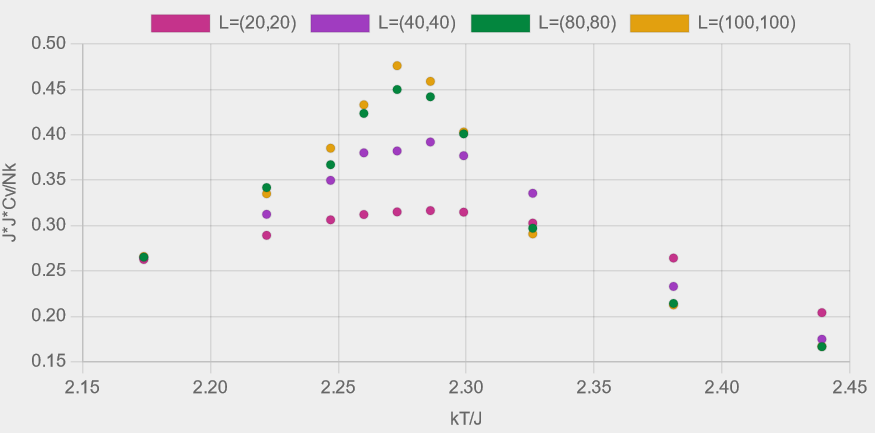
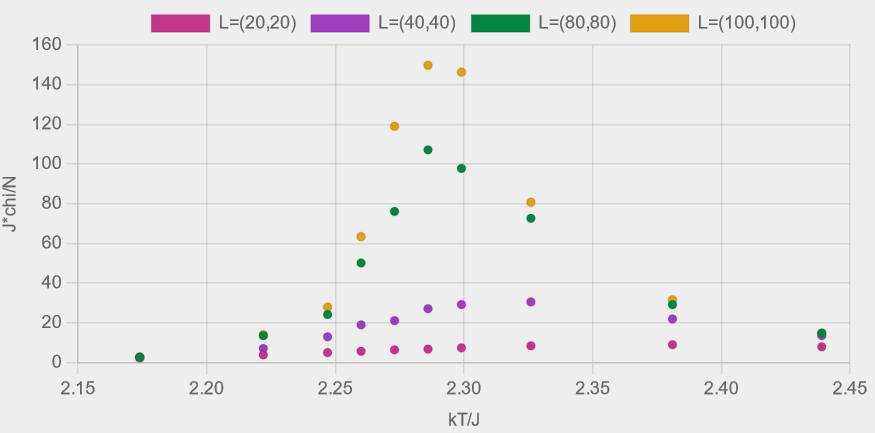
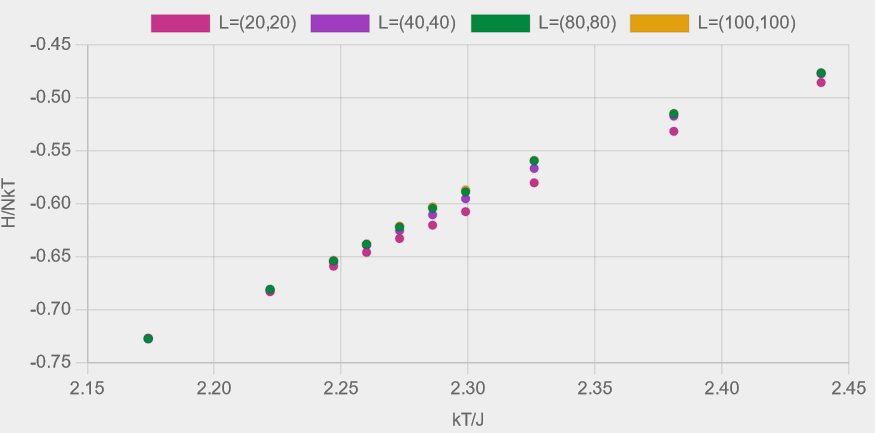
Figures 8 (a)-(e) show the results from experiments with four different lattice sizes, \( L=(20,20), (40,40), (80,80) \) and \( (100,100) \), each comprising ten Ising model simulations run at temperatures spanning the critical temperature.
The change in magnetisation across the transition clearly becomes steeper as lattice size increases towards an infinite system.
As well as the peaks in the heat capacity and suceptibility becoming taller and narrower, the temperature at which the peaks occur also shift closer to the critical temperature.
Figure 8 - Plots of (a) magnetisation, (b) Binder fourth-order cumulant, (c) heat capacity, (d) susceptibility and (e) energy, as described in table 2.
Each coloured dataset corresponds to a lattice of size \( L = (N_{x}, N_{y}) \).